一道小学数学题
今天群里看到一位家长发的小学数学题:
将数 1 到 10 填入下图,其中每个圆圈内的数字都不重复。将三条边上的四个数相加可以得到边长总和,已知三个边长总和都相同。
请问边长总和的最小可能值是多少?
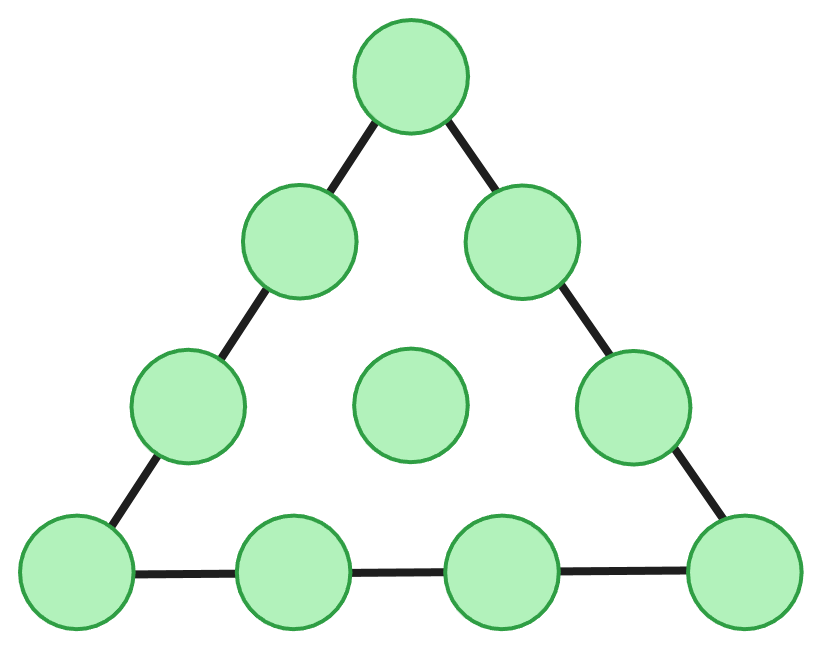
不知道数学老师会怎么讲解这道题,我这边也没想出来,但是作为程序猿,我们可以写代码列出所有可能的组合啊。
java
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Collectors;
import java.util.stream.IntStream;
public class Solution {
private int no = 1;
private int min = Integer.MAX_VALUE;
private int max = Integer.MIN_VALUE;
public static void main(String[] args) {
Solution solution = new Solution();
solution.initResult();
solution.calc(IntStream.rangeClosed(1, 10).toArray(), new ArrayList<>());
solution.printResult();
}
public void initResult() {
min = Integer.MAX_VALUE;
max = Integer.MIN_VALUE;
System.out.println("从顶点按顺时针或逆时针填如下数字(冒号前面为序号,结尾 -- 后面的是边长总和):\n");
}
public void printResult() {
System.out.printf("%n最小边长总和:%d%n最大边长总和:%d%n", min, max);
}
public void calc(int[] numbers, List<Integer> combination) {
if (combination.size() == 9) {
int l1 = combination.get(0) + combination.get(1) + combination.get(2) + combination.get(3);
int l2 = combination.get(3) + combination.get(4) + combination.get(5) + combination.get(6);
int l3 = combination.get(6) + combination.get(7) + combination.get(8) + combination.get(0);
if (l1 == l2 && l2 == l3) {
if (combination.get(0) > combination.get(3) || combination.get(3) > combination.get(6)) {
return;
}
if (combination.get(1) > combination.get(2) || combination.get(4) > combination.get(5) || combination.get(7) > combination.get(8)) {
return;
}
System.out.printf("%4d: %s -- %2d%n", no++, combination.stream().map(num -> String.format("%2d", num))
.collect(Collectors.joining(",")), l1);
min = Math.min(min, l1);
max = Math.max(max, l1);
}
} else {
for (int num : numbers) {
if (combination.contains(num)) {
continue;
}
combination.add(num);
calc(numbers, combination);
combination.remove(combination.size() - 1);
}
}
}
}这里排除了因为数字顺序不同的重复解,最终打印的结果如下:
plaintext
从顶点按顺时针或逆时针填如下数字(冒号前面为序号,结尾 -- 后面的是边长总和):
1: 1, 3,10, 6, 2, 5, 7, 4, 8 -- 20
2: 1, 4,10, 5, 2, 6, 7, 3, 9 -- 20
3: 1, 4,10, 6, 2, 5, 8, 3, 9 -- 21
4: 1, 5, 8, 6, 3, 4, 7, 2,10 -- 20
5: 1, 5, 9, 2, 4, 8, 3, 6, 7 -- 17
6: 1, 5, 9, 4, 2, 6, 7, 3, 8 -- 19
7: 1, 5, 9, 6, 3, 4, 8, 2,10 -- 21
8: 1, 5,10, 2, 3, 9, 4, 6, 7 -- 18
9: 1, 5,10, 2, 4, 9, 3, 6, 8 -- 18
10: 1, 6, 8, 2, 5, 7, 3, 4, 9 -- 17
11: 1, 6, 8, 4, 3, 5, 7, 2, 9 -- 19
12: 1, 6, 8, 5, 2, 4, 9, 3, 7 -- 20
13: 1, 6, 9, 2, 5, 7, 4, 3,10 -- 18
14: 1, 6, 9, 2, 5, 8, 3, 4,10 -- 18
15: 1, 6, 9, 5, 2, 4,10, 3, 7 -- 21
16: 1, 6, 9, 7, 3, 5, 8, 4,10 -- 23
17: 1, 6,10, 2, 4, 5, 8, 3, 7 -- 19
18: 1, 6,10, 2, 5, 9, 3, 7, 8 -- 19
19: 1, 6,10, 3, 4, 5, 8, 2, 9 -- 20
20: 1, 6,10, 4, 2, 7, 8, 3, 9 -- 21
21: 1, 6,10, 4, 3, 9, 5, 7, 8 -- 21
22: 1, 6,10, 5, 2, 7, 8, 4, 9 -- 22
23: 1, 7, 8, 3, 2,10, 4, 5, 9 -- 19
24: 1, 7, 8, 6, 3, 4, 9, 2,10 -- 22
25: 1, 7, 9, 2, 3,10, 4, 6, 8 -- 19
26: 1, 7, 9, 2, 4, 8, 5, 3,10 -- 19
27: 1, 7, 9, 2, 6, 8, 3, 5,10 -- 19
28: 1, 7, 9, 3, 2,10, 5, 6, 8 -- 20
29: 1, 7, 9, 4, 3, 6, 8, 2,10 -- 21
30: 1, 7, 9, 6, 2, 5,10, 4, 8 -- 23
31: 1, 7,10, 2, 3, 9, 6, 5, 8 -- 20
32: 1, 7,10, 2, 4, 9, 5, 6, 8 -- 20
33: 1, 7,10, 3, 4, 8, 6, 5, 9 -- 21
34: 1, 8, 9, 2, 5, 7, 6, 3,10 -- 20
35: 1, 8, 9, 2, 6, 7, 5, 4,10 -- 20
36: 1, 8, 9, 3, 5, 7, 6, 4,10 -- 21
37: 1, 8,10, 2, 3, 7, 9, 5, 6 -- 21
38: 1, 8,10, 3, 4, 6, 9, 5, 7 -- 22
39: 2, 4, 8, 9, 1, 3,10, 5, 6 -- 23
40: 2, 4, 9, 5, 1, 6, 8, 3, 7 -- 20
41: 2, 4,10, 5, 1, 6, 9, 3, 7 -- 21
42: 2, 4,10, 5, 1, 8, 7, 3, 9 -- 21
43: 2, 4,10, 6, 1, 7, 8, 3, 9 -- 22
44: 2, 5, 7, 8, 1, 3,10, 4, 6 -- 22
45: 2, 5, 9, 3, 1, 8, 7, 4, 6 -- 19
46: 2, 5, 9, 4, 3, 6, 7, 1,10 -- 20
47: 2, 5, 9, 6, 1, 8, 7, 3,10 -- 22
48: 2, 5,10, 6, 1, 7, 9, 4, 8 -- 23
49: 2, 6, 7, 5, 3, 4, 8, 1, 9 -- 20
50: 2, 6, 8, 3, 4, 5, 7, 1, 9 -- 19
51: 2, 6,10, 3, 1, 9, 8, 4, 7 -- 21
52: 2, 6,10, 3, 5, 9, 4, 7, 8 -- 21
53: 2, 6,10, 4, 1, 9, 8, 5, 7 -- 22
54: 2, 6,10, 5, 3, 7, 8, 4, 9 -- 23
55: 2, 7, 8, 5, 3, 4,10, 1, 9 -- 22
56: 2, 7, 9, 3, 4, 6, 8, 1,10 -- 21
57: 2, 7, 9, 3, 6, 8, 4, 5,10 -- 21
58: 2, 7, 9, 5, 4, 6, 8, 3,10 -- 23
59: 2, 7, 9, 6, 3, 5,10, 4, 8 -- 24
60: 3, 2, 9, 7, 1, 5, 8, 4, 6 -- 21
61: 3, 2,10, 5, 1, 8, 6, 4, 7 -- 20
62: 3, 2,10, 7, 1, 5, 9, 4, 6 -- 22
63: 3, 2,10, 8, 1, 5, 9, 4, 7 -- 23
64: 3, 4, 8, 5, 2, 6, 7, 1, 9 -- 20
65: 3, 4, 8, 5, 2, 7, 6, 1,10 -- 20
66: 3, 4, 8, 6, 1, 5, 9, 2, 7 -- 21
67: 3, 4, 9, 6, 1, 5,10, 2, 7 -- 22
68: 3, 4, 9, 6, 1, 8, 7, 2,10 -- 22
69: 3, 4, 9, 7, 1, 5,10, 2, 8 -- 23
70: 3, 4,10, 5, 1, 7, 9, 2, 8 -- 22
71: 3, 4,10, 6, 1, 9, 7, 5, 8 -- 23
72: 3, 5, 6, 7, 2, 4, 8, 1, 9 -- 21
73: 3, 5, 7, 6, 2, 4, 9, 1, 8 -- 21
74: 3, 5, 7, 8, 2, 4, 9, 1,10 -- 23
75: 3, 5, 8, 7, 2, 4,10, 1, 9 -- 23
76: 3, 5, 9, 4, 2, 8, 7, 1,10 -- 21
77: 3, 5,10, 6, 2, 7, 9, 4, 8 -- 24
78: 3, 6, 7, 8, 1, 5,10, 2, 9 -- 24
79: 3, 6, 7, 9, 1, 5,10, 4, 8 -- 25
80: 3, 6, 8, 4, 2, 5,10, 1, 7 -- 21
81: 3, 6, 8, 5, 1, 9, 7, 2,10 -- 22
82: 3, 6, 9, 5, 1, 7,10, 2, 8 -- 23
83: 3, 6,10, 4, 2, 9, 8, 5, 7 -- 23
84: 3, 7, 8, 5, 2, 6,10, 1, 9 -- 23
85: 3, 7, 8, 6, 4, 5, 9, 2,10 -- 24
86: 3, 7, 9, 4, 5, 6, 8, 2,10 -- 23
87: 4, 1,10, 6, 3, 5, 7, 2, 8 -- 21
88: 4, 2, 9, 5, 1, 8, 6, 3, 7 -- 20
89: 4, 2,10, 5, 1, 7, 8, 3, 6 -- 21
90: 4, 2,10, 5, 1, 9, 6, 3, 8 -- 21
91: 4, 2,10, 5, 3, 6, 7, 1, 9 -- 21
92: 4, 2,10, 6, 3, 5, 8, 1, 9 -- 22
93: 4, 3, 8, 5, 2, 7, 6, 1, 9 -- 20
94: 4, 3, 9, 5, 2, 8, 6, 1,10 -- 21
95: 4, 3, 9, 7, 2, 6, 8, 1,10 -- 23
96: 4, 3,10, 5, 2, 6, 9, 1, 8 -- 22
97: 4, 3,10, 5, 2, 7, 8, 1, 9 -- 22
98: 4, 3,10, 6, 1, 7, 9, 2, 8 -- 23
99: 4, 3,10, 8, 2, 6, 9, 5, 7 -- 25
100: 4, 5, 8, 6, 1, 9, 7, 2,10 -- 23
101: 4, 5, 8, 7, 2, 6, 9, 1,10 -- 24
102: 4, 5, 9, 6, 1, 7,10, 2, 8 -- 24
103: 4, 5, 9, 6, 3, 7, 8, 2,10 -- 24
104: 4, 5, 9, 7, 2, 6,10, 3, 8 -- 25
105: 4, 6, 7, 8, 3, 5, 9, 2,10 -- 25
106: 4, 6, 8, 5, 1,10, 7, 3, 9 -- 23
107: 4, 6, 8, 7, 3, 5,10, 2, 9 -- 25
108: 4, 6, 9, 5, 1, 8,10, 3, 7 -- 24
109: 4, 7, 8, 5, 3, 6,10, 1, 9 -- 24
110: 5, 2, 8, 9, 1, 4,10, 3, 6 -- 24
111: 5, 2,10, 6, 1, 9, 7, 3, 8 -- 23
112: 5, 3, 7, 8, 1, 4,10, 2, 6 -- 23
113: 5, 3, 9, 6, 2, 8, 7, 1,10 -- 23
114: 5, 3,10, 6, 1, 9, 8, 4, 7 -- 24
115: 5, 3,10, 6, 2, 9, 7, 4, 8 -- 24
116: 5, 4, 6, 8, 2, 3,10, 1, 7 -- 23
117: 5, 4, 6, 9, 2, 3,10, 1, 8 -- 24
118: 5, 4, 9, 6, 3, 7, 8, 1,10 -- 24
119: 5, 4, 9, 6, 3, 8, 7, 2,10 -- 24
120: 6, 1, 9, 8, 2, 4,10, 3, 5 -- 24
121: 6, 2, 7, 9, 1, 4,10, 3, 5 -- 24
122: 6, 2, 8, 7, 1, 5,10, 3, 4 -- 23
123: 6, 3, 7, 9, 2, 4,10, 1, 8 -- 25
124: 6, 4, 5, 9, 2, 3,10, 1, 7 -- 24
125: 7, 1, 8, 9, 2, 4,10, 3, 5 -- 25
126: 7, 1, 9, 8, 3, 4,10, 2, 6 -- 25
127: 7, 2, 6, 8, 1, 5, 9, 3, 4 -- 23
128: 7, 2, 8, 9, 1, 6,10, 4, 5 -- 26
129: 7, 3, 5, 8, 2, 4, 9, 1, 6 -- 23
130: 7, 4, 6, 9, 2, 5,10, 1, 8 -- 26
131: 8, 2, 6, 9, 1, 5,10, 3, 4 -- 25
132: 8, 2, 7, 9, 1, 6,10, 3, 5 -- 26
133: 8, 3, 5, 9, 2, 4,10, 1, 6 -- 25
134: 8, 3, 6, 9, 2, 5,10, 1, 7 -- 26
135: 8, 3, 7, 9, 2, 6,10, 4, 5 -- 27
136: 8, 4, 6, 9, 3, 5,10, 2, 7 -- 27
最小边长总和: 17
最大边长总和: 27根据结果可以看到,对于这个三角形的三个顶点,任意数字组合都是有解的。
以此反推的话,感觉这题可以这样解释:
- 边长总和 = (9 个数字的和 + 顶点的三个数字的和)
3 - 因此,边长最小的时候就是:选择的 9 个数字最小,另外顶点的三个数字的和最小
- 也就是选择的 9 个数字排除 10,然后顶点的三个数字选择 1,2,3
- 此时只有两种可能的组合,边长总和都为 17plaintext
5: 1, 5, 9, 2, 4, 8, 3, 6, 7 -- 17 10: 1, 6, 8, 2, 5, 7, 3, 4, 9 -- 17
反之,这题如果求的是最大可能值,求解过程也是类似的。
- 选择的 9 个数字排除最小的 1,三个顶点选择 8,9,10
- 此时只有如下两种组合,边长总和都为 27plaintext
135: 8, 3, 7, 9, 2, 6,10, 4, 5 -- 27 136: 8, 4, 6, 9, 3, 5,10, 2, 7 -- 27
